
堆排序相对稳定,最优和最差复杂度都是O(nlogn)[一共调整n次堆,每次复杂度为logn]。相比之下,快速排序在最差情况即基本逆序时,复杂度无异于冒泡排序O(n*n)[每趟排序复杂度为n,分治失效故排n次];而冒泡排序在基本有序时,只需扫描一次,复杂度为O(n)。所以堆排序适用于更关注最差复杂度的情况。同时,取堆顶操作,可以降低取无序数组最小K个元素的复杂度为K*logn。
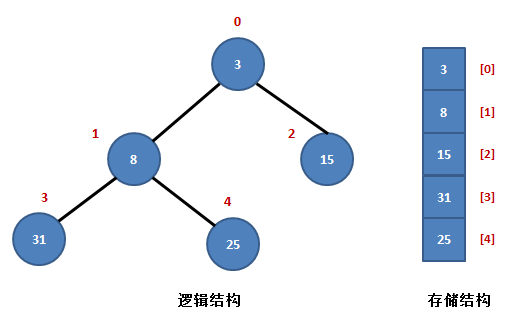
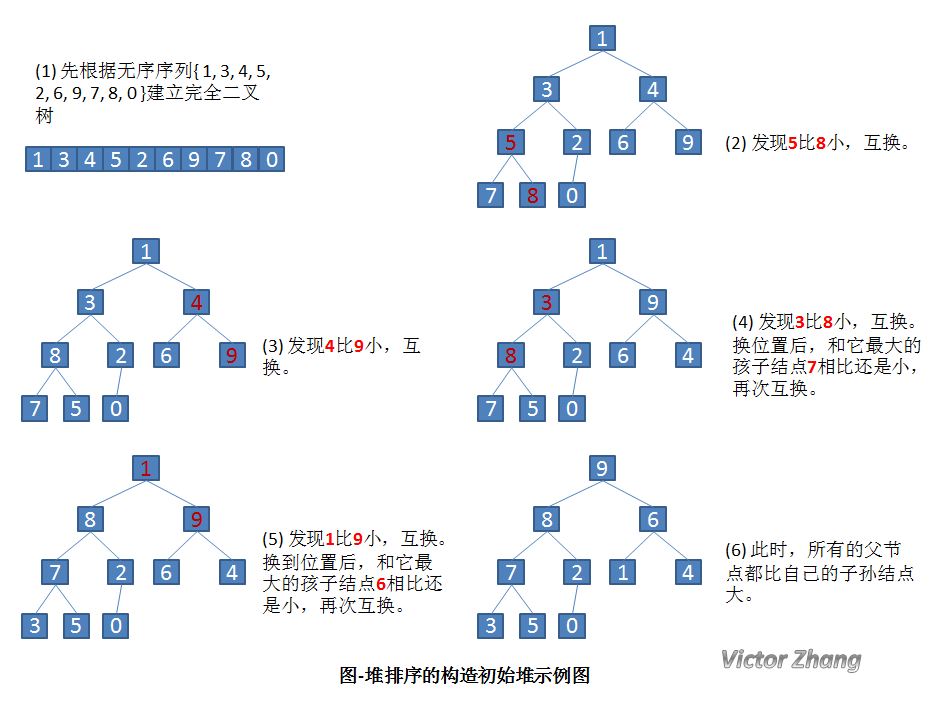
堆排序主要分两步:调整,即建堆,从当前根起让每个父节点不大于子节点,调整必须是自底向上的,最后一个非叶子节点是length/2-1;输出,即将堆顶元素与数列最后一个元素交换,再不断调整(数列长度-1)。
#includeusing namespace std;void HeapAdjust(int arr[], int i, int nLength){//调整i节点为根的子堆 int child; for (; 2 * i + 1 < nLength; i = child){ //这个循环是有必要的,自上向下调整该子树 if (i <= nLength / 2 - 1){ child = 2 * i + 1; if (child + 1 < nLength&&arr[child] > arr[child + 1]){ child++; //只和较大的交换,即只破坏了较小子树的平衡,这样才有log n的复杂度 } if (arr[child] < arr[i]){ int temp = arr[i]; arr[i] = arr[child]; arr[child] = temp; } else break; } }}/*int HeapTop(int arr[], int *nLength){ //堆必须从下往上调整 int l = *nLength, temp; for (int i = l / 2 - 1; i >= 0; i--){ HeapAdjust(arr, i, l); } temp = arr[0]; arr[0] = arr[l - 1]; arr[l-1] = temp; l--; *nLength = l; return arr[l];}void HeapSort(int arr[],int length, int b[]){ //利用HeapTop排序 int l = length; for (int i = 0; i < length; i++){ b[i] = HeapTop(arr, &l); }}*/void HeapSort(int array[], int length) //直接排序?可以这样吗,可以{ int i; for (i = length / 2 - 1; i >= 0; --i) HeapAdjust(array, i, length); //堆顶最小 for (i = length - 1; i>0; --i) //把堆顶和堆底交换,实际上是逆调整顺序输出,依旧自底向上 { int temp; temp = array[i]; array[i] = array[0]; array[0] = temp; HeapAdjust(array, 0, i); //从顶开始调整,HeapAdjust()中循环的意义 } for (int i = 0; i < length / 2;i++){ //如果HeapAdjust()改为大在上,则无需此循环 int temp; temp = array[i]; array[i] = array[length - 1 - i]; array[length - 1 - i] = temp; }}int main(){ int arr[] = {49,31,22,76,32,45,61,21,13,58,49 }; int length = sizeof(arr) / sizeof(int); int b[100]; HeapSort(arr, length, b); for (int i = 0; i < sizeof(arr) / sizeof(int); i++) cout << b[i] << " "; cout << endl; HeapSort(arr, length); for (int i = 0; i < sizeof(arr) / sizeof(int); i++) cout << arr[i] << " "; return 0;}